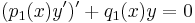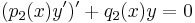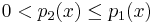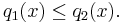Sturm–Picone comparison theorem
In mathematics, in the field of ordinary differential equations, the Sturm–Picone comparison theorem, named after Jacques Charles François Sturm and Mauro Picone, is a classical theorem which provides criteria for the oscillation and non-oscillation of solutions of certain linear differential equations.
Sturm–Picone comparison theorem
Let
be two homogeneous linear second order differential equations in self-adjoint form with
and
Let u be a non-trivial solution of (1) with successive roots at z1 and z2 and let v be a non-trivial solution of (2). Then one of the following properties holds.
- There exists an x in [z1, z2] such that v(x) = 0; or
- there exists a λ in R such that v(x) = λ u(x).
In the special case where both equations are equal one obtains the Sturm separation theorem.
References
- Diaz, J. B.; McLaughlin, Joyce R. Sturm comparison theorems for ordinary and partial differential equations. Bull. Amer. Math. Soc. 75 1969 335–339 pdf
- Heinrich Guggenheimer (1977) Applicable Geometry, page 79, Krieger, Huntington ISBN 0882753681 .
- Teschl, Gerald (2011). Ordinary Differential Equations and Dynamical Systems. American Mathematical Society. http://www.mat.univie.ac.at/~gerald/ftp/book-ode/.